毕业好难(一)
大体框架
首先是将终端和卫星都统一到地心惯性坐标系(ECI)中,这个坐标系的特点是不随地球的自转而运动,终端和卫星在这个坐标系中的速度就是相对于静止物体的速度,可以由此速度计算卫星与终端之间的多普勒,也可以算出星地距离、俯仰角方位角等。
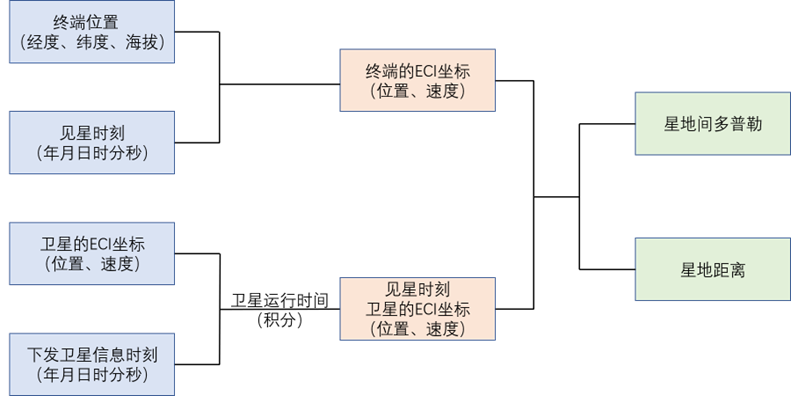
终端的位置可以根据终端的经纬度以及海拔高度将其固定在ECEF坐标系中,ECEF坐标系是随着地球自转而转动的坐标系,然后再根据公示将其转换到ECI坐标系中。
卫星的位置则根据轨道六根数将卫星的状态映射到ECI坐标系中。
轨道六根数
卫星的轨道六根数是用于表征卫星轨道形状、位置及运动等属性的参数,可用来确定任意时刻卫星的轨道和位置。轨道六根数指的是:轨道半长轴$\alpha$,轨道离心率$e$,轨道倾角$i$,近心点辐角$\omega$,升交点经度$\Omega$和真近点角$\theta$.
其中轨道半长轴和轨道离心率都是椭圆轨道的参数,和椭圆中的离心率和半长轴是一样的定义。
轨道倾角
轨道倾角$i$是指在惯性坐标系中,例如在ECI中,轨道的正法向与z轴的夹角,轨道的正法向指的是按照右手螺旋定则垂直于轨道的平面的方向。轨道倾角$i$的取值范围是[0,180].
近心点辐角
近心点辐角$\omega$是指离心率矢量与升交线的夹角。卫星自下而上穿过赤道面的点称作升交点,地心与升交点的连线就是升交线。离心率矢量则是地心到近地点的向量。近心点辐角$\omega$的取值范围是[0,360].
升交点经度
升交点经度$\Omega$指的是升交线与坐标系x轴的夹角,范围是[0,360].
真近点角
真近点角$\theta$指的是离心率矢量到卫星位置矢量的夹角,范围是[0,360].
在轨道六根数中,前两项决定了轨道形状,第3、4、5项确定了轨道所处的位置,最后一项决定了卫星在轨道中的位置。